Az empirikus megismerésnek a statisztika az egyik legfontosabb eszköze. A statisztikának a mindenki által ismert és tanult változata a klasszikus (frekventista) iskola. Van azonban egy másik is, a Bayesi iskola, amelynek gyakorlati alkalmazását egyre inkább lehetővé teszi a számítógépek számítási kapacitásának, és gyorsaságának fejlődése. A Bayesi statisztika más filozófiai szemléletmóddal és elméleti megközelítéssel rendelkezik. Valójában mi a célja a statisztikának? Miben különbözik a két iskola ismeretelméleti alapokban, feltételezésekben és módszertanban? Ezeket a kérdéseket érdemes megválaszolni, hogy megértsük a Bayesi módszer lényegét.
A statisztika segíti a világ általunk való megismerését és megértését, továbbá eszközt nyújt a tudományos vizsgálatnak, és támogatni tudja a döntéshozási folyamatokat. Keretet ad az adatok szisztematikus rendszerezésére, elemzésére, értelmezésére, és lehetőséget nyújt megbízható következtetések levonására. Episztemológiai értelemben véve a célja tehát az, hogy megfigyelések alapján felfedjen mintázatokat, általánosságokat, és korábban nem ismert összefüggéseket, valamilyen tudást a világról.
Ha azonban mélyebben belegondolunk, akkor felmerülhet a kérdés, hogy hogyan lehet egyáltalán megismerni a világot. Immanuel Kant, a nyugati világ egyik legnagyobb hatású filozófusa szerint a világ megértése nem csak azon múlik, hogy közvetlenül mit érzékelünk belőle, hanem annak is aktív szerepe van, hogy az elménk hogyan értelmezi a megfigyelt jelenségeket, és milyen kategóriákat rendel azokhoz. Szerinte nincs közvetlen, filter nélküli rálátásunk arra, hogy a világ milyen valójában. Ez az elménk már eleve adott struktúrája miatt van, amely minden tapasztalatot már egy adott keretrendszerben értelmez. Emiatt két különböző dolog az, hogy a dolgok milyenek valójában, és az, hogy a megjelenésüket hogyan értelmezzük. A világról alkotott tudásunk tehát a világnak csak egy elménk általi reprezentációja. Mindebből az következik, hogy nincs tiszta megismerés, a világot nem lehet úgy megismerni, hogy nincs valamilyen előzetes feltételezésünk vagy prekoncepciónk a világról.
Ezzel szemben van egy másik megközelítés, amely mellett John Locke, az empirizmus egyik nagy filozófusa érvelt. Ő elvetette azt, hogy szükséges lenne előzetes tudás a világ megismeréséhez, és azt mondta, hogy az elménk kezdetben egy „tiszta tábla” (tabula rasa), azaz az ember nem rendelkezik semmilyen veleszületett ideával. A tudás tehát egyszerű ideák empirikus megfigyelésén és megtapasztalásán keresztül jön létre, az összetettebb tudás pedig ezen egyszerű ideák kombinálásával és absztrakciójával alakul ki. A lényeg tehát az, hogy Locke filozófiája szerint a világ megismerhető úgy, ahogy van valójában, és ehhez nincs szükség előzetes feltevésekre.
Egy matematikai modellt általában azért hozunk létre, mert azzal valahogyan reprezentálni, leírni szeretnénk a valóság egy szeletét, egy rendszer működését, egy jelenséget. Egy modellben vannak változók, amelyek egy rendszer tulajdonságait vagy állapotát írják le. Az egyenletrendszerek megadják, hogy milyen struktúrában keressük a változók közötti összefüggéseket. Végül a paraméterek megválasztásával lehet megvalósítani, hogy a kívánt formába kerüljön, adott célhoz illeszkedjen a modell, ami általában azt jelenti, hogy a modell írja le azt, ahogy a valóságban megfigyeljük a dolgokat. A statisztika célja az, hogy megfigyelt adatok segítségével úgy becsülje meg egy modell paraméterit, hogy azokkal a modell minél pontosabb leírását adja a valóságnak.
A klasszikus (frekventista) statisztika, mint tudományág a 20. század elején született Locke szemléletmódját követve. Arra a feltételezésre épül, hogy a világban minden objektum jellemezhető valószínűségi-eloszlásokkal, és minden megfigyelés egy valószínűségi változónak a realizációja. Az adat tehát egy véletlen minta a potenciális realizációk végtelen populációjából, és azt a fix paraméterkombinációt keressük, amelyről a legvalószínűbb, hogy generálta az adatot. Erre a paraméterkombinációra egy pontbecslést adunk, azaz fix értékeket.
Ezzel szemben a Bayesi iskola, amely néhány évtizeddel később született, az adatot veszi adottnak, és a paraméterek a véletlen változók, más szóval valószínűségi eloszlások, azaz nem fix értékek. A Bayesi becslés tehát a paramétertér minden eleméhez egy valószínűséget rendel. A Bayesi (adatból való) tanulás egy egyszerű és elegáns módszeren alapul, és megértéséhez három valószínűségi-eloszlást kell ismerni, amelyeken keresztül látható, hogy miért Kant megismerés elméletéhez áll közel ez a statisztikai iskola. Ezek egydimenziós paramétertérben ábrázolva az alábbi ábrán láthatók.
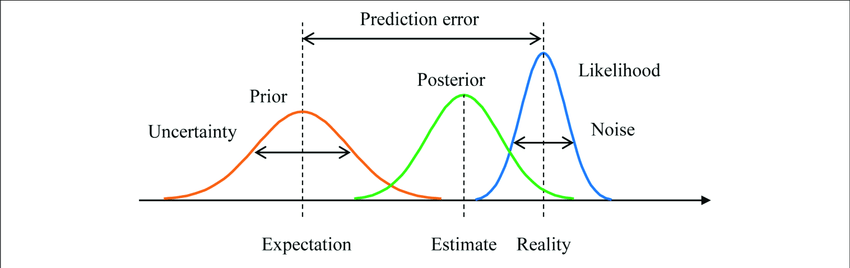
Forrás: researchgate.net
Kezdetben mielőtt bármit látnánk az adatból, van egy feltételezésünk arról, hogy nagyjából milyen értéket vehetnek a paraméterek. Ezt a pirossal ábrázolt prior eloszlás testesíti meg, és a paramétertér minden eleméről ad egy vélekedést, hogy az mennyire valószínű az előzetes tudásunk alapján. Ezzel azt is meg tudjuk adni, hogy mennyire vagyunk biztosak a vélekedésünkben, továbbá akár ki is zárhatunk olyan kimeneteleket, amiket lehetetlennek tartunk. Ez utóbbi azért hasznos, mert kevesebb lehetséges paraméterkombináció esetén elég kisebb számítási kapacitás, és így rövidebb idő az optimális paraméterek megtalálásához.
A második fontos eloszlás a kékkel ábrázolt likelihood függvény, amely már a megfigyelt adatokhoz tartozik, és a paraméterek függvénye. Tehát egy feltételes eloszlás, amely megmutatja, hogy adott paraméter mellett mekkora a valószínűsége, hogy azt az adatot látjuk, amit látunk. Itt is megmutatkozik, hogy az adat fix, és a paraméter a véletlen változó.
Van tehát egy eloszlásunk arról, hogy mi a kezdeti elképzelésünk a paraméterekről, és egy arról, hogy mit látunk az adatokból. Itt használjuk fel a Bayes-tételt[1], amivel priorból és a likelihoodból megkapjuk zölddel ábrázolt, úgynevezett posterior eloszlást, amely a „Bayesi tanulás” eredménye. Tanulás alatt azt értjük, hogy az előzetes vélekedésünket frissítjük a látott adatok alapján. A posterior is egy feltételes eloszlás, amely minden lehetséges paraméterkombinációról megmutatja, hogy az a tanulás után mennyire valószínű, feltéve a látott adatokat.
Ahhoz tehát, hogy Bayesi módszerrel próbáljuk meg megismerni egy rendszer működését, szükséges, hogy legyen egy akár biztos, akár bizonytalan priori elképzelésünk a rendszerről. Így ez a módszer kifejezetten hasznos olyankor, amikor olyan ismeret birtokában vagyunk, ami nem mérhető, és nem figyelhető meg közvetlenül adatokon, mert így ezt is be lehet építeni a becslésbe. Az eredmény pedig nem egy adott paraméter érték, hanem egy valószínűségi eloszlás, amivel számszerűsíthető és menedzselhető a becslés bizonytalansága. Ami miatt még kifejezetten hasznos tud lenni egyes esetekben az az, hogy kis minta is elég, hogy értelmes becslést kapjunk. Ilyenkor azonban gondosan meg kell fontolni a prior eloszlást, és a modell specifikációt. Egy probléma viszont, hogy nem mindig nyerhető ki a posterior eloszlás analitikus módon, és szimulációt kell használni, hogy megkapjuk. Összességében nem mondható, hogy egyik módszer jobb lenne a másiknál, érdemes mindkettőt ismerni, és mindig az adott problémához legjobban illőt választani.
A Bayesi módszer tehát a modern statisztikában testesít meg egy többszáz éves episztemológiai megközelítést. Segíti a bizonytalanság, az adathiány és bonyolultság kezelését, továbbá hasznos modell összehasonlításhoz és prior információk beépítéséhez. Egyre nagyobb szerepe van a gépi tanulás területén, így használata elterjedt például az orvostudományban, a bioinformatikában, a robotikában, a termékfejlesztésben, a pénzügyi idősorok vagy éppen az időjárás előrejelzésében.
0 hozzászólás